STM 308
Matrix Algebra with Applications
Linear Equations and Systems
A Linear equation has some set of variables.
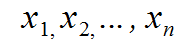
These variables are an equation of the form:
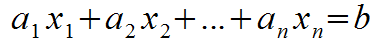
Why Linear?
Because we don't deal with curves. No spheres. No parabolas.
The number of variables the system has determines the number of dimensions the resulting solution will have.
- R2 means 2 variables (n = 2) so it's a line but results in a point.
- R3 means 3 variables, so it's a plane but results in a line.
- R4 means 4 variables, so it's a hyper-plane (?), but results in a cube.
Linear System
Example:
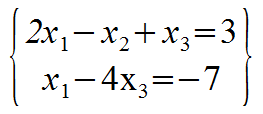
In this system, there are 2 equations and 3 unknowns. The size of this system is 2 by 3 (2x3). 4x5 is 4 equations, 5 unknowns.
Refer to the columns as x1 column, and solution column.
An example solution is the triple (5, 10, 3).
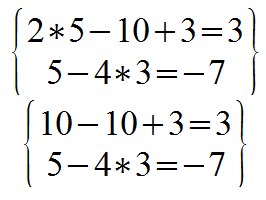
The long form of Rn systems are:
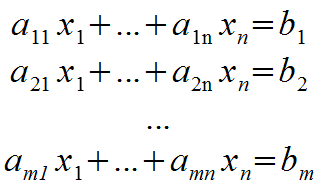
The solution is expressed as:
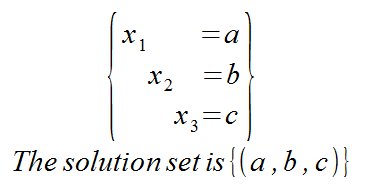
Row Operations
- Row Interchange
- Ri (Row-number (equation number) ← Rj.
- Swap row-i and row-j
- Undo: Ri ← Rj
- Row Scaling
- Ri ← cRi where c ≠ 0
- When c=0, this removes an equation thus creates a new system.
- Undo: Ri ← 1/c Ri
- Row Replacement
- Ri ← Ri + C Rj
- C can be 0, but that's complicated, so avoid it.
- Undo: Ri ← Ri - C Rj
Here is the simplest, easiest, solved Linear System that's a size of 3x3:
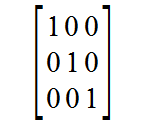
Any other 3x3 Linear System can be transformed into this System using the row operations.
A much cleaner verison excludes the variables. This is called a coefficient Matrix and it looks much more similar to happy matricies of youth and 3D programming.
Row operations are reversible.
Inconsistent solutions
If the augmented form of a Linear System has a row of the for [0 ... 0 | b] where b ≠ 0, then the Linear System is consistent.
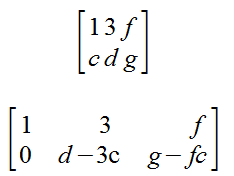
The only time this matrix is inconsistent is if d-3c == 0 and g-fc ≠ 0, because then a zero-row has a non-zero value, which is mathematically impossible.
Theory
Basic properties of real numbers.
- If a, b, c are real numbers, where c ≠ 0, then a=b ↔ ac = bc
- This goes both ways. This is how we can justify Row Scaling.
- If a, b, c, d are real numbers and a=b and c=d then a+c = b+d
- This does not go both ways. It is an if-statement. So if the result is true, it does not necicarilly mean the condition is true.
The reversibility of the row operations along with the basic properties above, ensures that the solution sets of row-equivalent linear systems are the same.
Matricies
- Matricies are denoted by capital letters with the entries enclosed with square brackets.
- If A is an mxn matrix, then the entry in the (i, j)-positon is denoted by aij
- Matrix
- Zero Row
- Non-Zero Row
- Echelon Form
- Reduced Echelon Form
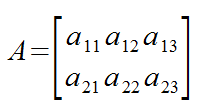
Theorem
If A is an mxn matrix, then there exists a unique matrix U in reduced echelon form such that A ~ U.
If A ~ U and U is in echelon form, then we call U an echelon form of A; if U is in reduced ecehlon form, then we call U the reduced ecehlon form of A. We specify an versus the because reduced ecehlon form is unique, but regular echelon is not unique.
Types of Solutions
- Inconsistent
- A zero-row has a non-zero value in the solution column.
- Unique
- Every column in the coefficient matrix is a pivot column.
- Infinite
- Presence of free variables, that is, one of the columns of the coefficient matrix is not a pivot column.
Example:
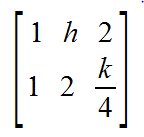
- Inconsistent if h = 2 and k ≠ 8
- Unique if h ≠ 2. k can be anything, so we don't specify it at all.
- Infinite if h = 2 and k = 8.
Vectors
Literally just a matrix with a single column. The number of row corresponds to the number of dimensions the system is in.
Addition
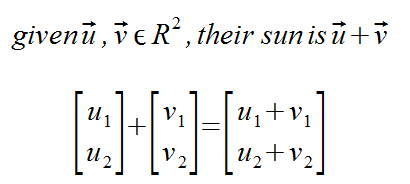
Scalar Multiplication
Literally just multiply each entry by the same real number.
Translation
Algebraic Properties of Rn
- Commutative. Reverse-order doesn't matter. A + B = B + A
- Associative. Doesn't matter which order you add. (A + B) + C = A + (B + C)
- A + 0 = A = 0 + A
- A + (-A) = (-A) + A = 0
- -A := -1 * A
- c(A + B) = cA + cB
- (c+d)A = cA + dA
- c(dA) = (cd)A
- 1A = A
We prove this because these properties apply to real numbers, and vector-addition is simply adding real numbers (the vector's entries), so there we go!
Linear Combinations
Given vectors v1, ..., vp in Rn and scalars c1, ..., Cp in R, the vector y is defined by:
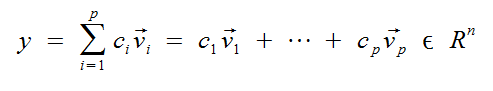
This is called the Linear Combination of v1, ..., vp w.r.t. the scalers c1, ..., cp.
We can prove that a sum of vectors multiplied by scalars can be transformed into, and thus equals, a Linear System.
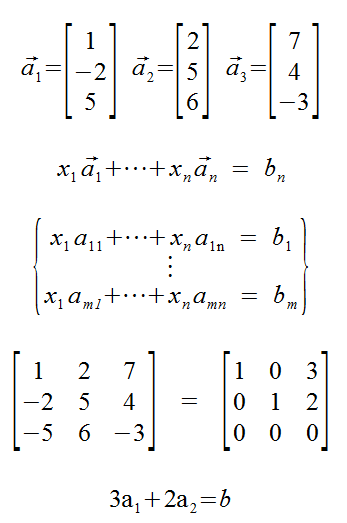
Span
Properties
- Span ({v1, ..., vp}) contains v1, ..., vp.
- vector 0m in span ({v1, ..., vp}). All scalars are 0 results in a zero vector.
- Determing whether vector a: [a1 ... an | b] is feasible, is equal to determining whether vector b is in span({a1, ..., an})
The Matrix Equation
Ax = b, where x and b are vectors.
if 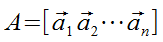
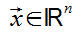
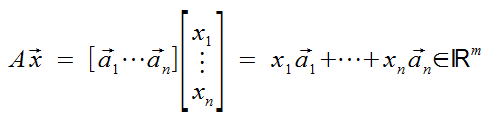
This results in transforming vectors into different dimensions unless m=n!
This is simply, nothing more, than a shorthand name for what we did with vectors above where we scaled them then added them together. This is literally a function as in programming functions. Now we just need to write Ax = b instead of that giant mess.
Even more simply put: this is vector-addition where the columns of a matrix are trated as a series of vectors, and each vector is multipled by values in another vector. The sum is our result. Easy peasy!
An mxn matrix A determines a function: TA : Rn → Rm and vector x in Rn → Ax in Rm.
The "product" Ax defines a function (mapping) from Rn to Rm.
TA:Rn → Rm means to send x → Ax. We are sending a vector to another dimension!
What it means to solve
Given some Matrix A, we have a destination matrix b in space Rm that we want, so we find a vector x in space Rn that will result the vector b.
In 3D worlds, this means having a vertex in 4D space, multiplying it by a matrix that will result in the vertex either appearing in our 3D world, or not.
Theorem
We can find a vector b in the span of vectors a, but can we find a vector b with any value? Do some values not work? In other words, will the system be inconsistent? No. It can be inconsistent.
We need a pivot in every row of A for every vector b to be in the span of vectors a (matrix A).
The columns of A span Rm if every vector b in Rm is a linear combination of the columns of A.
Theorem
If A is an mxn matrix, then the following statements are equivalent. (they are all true, or all false).
- Ax = b is consistent for every vector b in Rm.
- b is in the span of vectors a
- The columns of A span Rm (Rm = span of vectors a)
- The Reduced Echelon Form of A has a pivot position in every row.
Theorem
If A is an mxn matrix, then vectors u and v in Rn and scalar c in R, then:
- A(u + v) = Au + Av
- A(cu) + c(Au)
This fails for functions like y=x2, but works here because we're doing Linear algebra.
The proof is A(u+v) is equal to (u1 v1)a1... Split this out to multiple u1A1 + v1A1... Now rearrange them so u's are together and v's are together, now we can pull 'u' and 'v' out to form Au Av!!
Special Tranfom Matricies
The identity matrix: taking a vector and mapping it to itself.
Permutation Matrix, all 1s and 0s, but in odd ways to move the values of x around. Rearrangement.
Projection Matricies. All 1s and 0s, but one row is all 0s so the x-vector will simply be projected down to a lower dimension. This is an over-simplified projection where we literally throw out a dimension of data, and the rest of the axis will be projected down.
Solution Sets of L.S.
This is an example of a homogeneous linear system and its solution. If the solution is not unique, then it is a span.
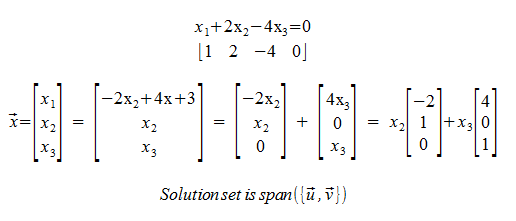
The homogeneous linear system is the base vector. That is, one that goes through the origin. Non-homogeneous linear systems are just this base linear system shifted somewhere.
Theorem
There exists vectors v1, ..., vp such that the solution set to Ax = 0 is span ({v1, ..., vp}).
Parametric Vector Equation
Yet another way to write down a linear system. Shows how Linear Systems can be translated. The resulting coefficient matrix is the homogeneous Linear System, and the added vector shows translation!
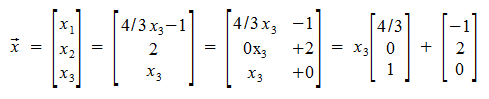
Theorem
Suppose Ax = b is consistent for some (maybe not all) b in Rm and let vector p in Rn be a solution. Then the solution set of all Ax = b are vectors of the form w = v + p where vector v is any solution of Ax = 0.
In other words, (Ax = b) == (v + p) where p is in the span x, and v means the vector x in the homogeneous system Ax = 0.
Trivially, this vector x could always be all 0s. Non-trivially, there may be a situation where a non-zero vector results in Ax == 0. These solutions could also be used as 'v' in our simplification above.
Proof
If w = v + p, then Aw = A(v + p) = Av + Ap = 0 + b = b! Going backwards, suppose another solution to Ax = b is 's'. s = s - p + p → (s-p) + p. Notice that A(s - p) = As - Ap = b - b = 0!! Wow!
Linear (In)dependence
Remember that the Matrix Equation Ax=b is another way to write a sum of vector multiplication.
If you have a linearly dependent set, this means you have a vector in the set that's already covered in the span of those vectors. This means this vector is a linear combination of the other vectors.
What we're trying to say is that we can remove this vector without affecting the span the entire set represents.
The vectors a are linearly independent if, and only if, the homogeneous matrix A has only the trivial solution.
Example: Are the vectors below Linearly Independent? If not, find an Linear Dependence Relation.

Instead of homogeneous systems with trivial or non-trivial solutions, we're looking at vectors and calling it Linearly Dependence or Linearly Independence.
Proposition
The set of a single vector v: {v}, is Linearly Independent iff the vector v does not equal 0.
The set {v1, v2} is L.D. iff v1 = c v2, where c is any constant.
Proof
(←) If v1 = c v2, then v1 - c v2 = 0, so that the set {v1, v2} is L.D.
(→) If {v1, v2} is L.D., then there exists scalars c1 and c2 (not both zero) such that c1 v1 + c2 v2 = 0. Assume c1 is not 0. Then v1 = c2/c1 v2.
Theorem
The set S = {v1, ..., vp}, where p >= 2, is L.D. if and only if at least one of the vectors in S is a linear combination of the others.
Proof
(←) Suppose that vj = c1 v1 + ... + cj-1 vj-1 + cj+1 vj+1 + ... + cp vp. Then 0 = c1 v1 + ... + cj-1 vj-1 - vj + cj+1 vj+1 + ... + cp vp so that S id L.D.
(→) Suppose that S is L.D. Then there exists scalars c1, ..., cp (not all 0) such that c1 v1 + ... + cp vp = 0. Suppose cj is the first non-zero scalar. Then vj = c1 / -1cj v1 + ... + what we did above. We subtract everything execpt vj and then divide by cj.
What we're doing here
A L.D. tells us that we have a redundency in our span of vectors, so we can remove at least one of them. And it doesn't matter which vector we remove from the span because any Linear Combination of the other vectors will still result in the same span.
Theorem
If Set S = vectors v through p in Rn and p >n, then S is L.D.
Proof
The L.S. [v through vp] is underdetermined (more columns than rows), and therefore cannot have a pivot position in every column and cannot have a unique solution.
Theorem
If S (as above) but now a Zero-Vector is in S, then S is L.D.
Proof
Assume v1 = 0, then 1v1 + 0v2 + ... + 0vp = 0.
In summary
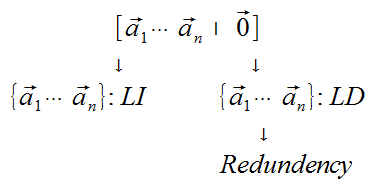
This generalizes what we're saying, where the set of vectors either has a trivial solution for 0, or inifinite solutions for 0.
Linear Transformations
Consider a function T that maps Rn into Rm. This takes some vector x in Rm and results in Ax in Rm.
When we solve a linear system Ax = b, we're just solving for this vector x to find the original vector x that results in the vector b.
Because T(x) = Ax, this means the same properties that apply to te Matrix Equation apply to this function T.
- T(x + y) = T(x) + T(y)
- T(cx) = c T(x)
Example:


Proposition
(assuming we no nothing about T...) What is a linear transformation? What does it mean to be linear?
If T maps Rn to Rm, then T is linear if (not only if) T(0n) = 0m.
If T maps Rn to Rm is a function, then T is linear iff T(cx + dy) = cT(x) + dT(y)
Proof
Because T(cu) = c T(u) for every c in R, notice that T(0n) = T(0 u) = 0 T(u) = 0m
→ because of what we just proved above (we can take out constants/scalars).
← Because T(1x +1y) = 1T(x) + 1T(y) = T(x) + T(y). And T(cx) = T(cx + 0y) = cT(x) + 0T(y) = cT(x)
Example. Determine whether the following are linear:
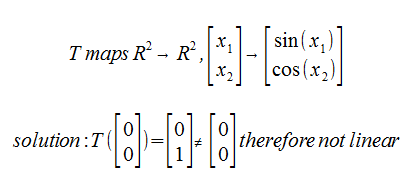
What is the rotation matrix?
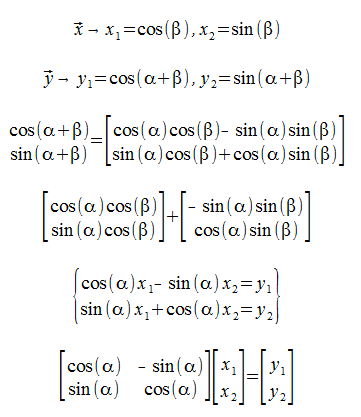
Matrix of a Linear TF
Theorem
Let T: Rn → Rm be a linear transformation, then there exists a unique matrix A such that T(x) = Ax
Moreover, if ej denotes the jth-column of the nxn identity matrix I, then A = [T(e1) ... T(en)].
We're stating that any Linear transformation is (and thus can be written as) a Matrix Transformation.
Proof
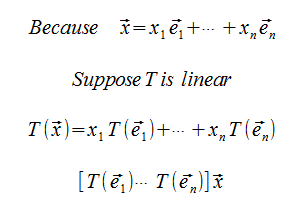
Matrix Operations
Matrix Algebra
Algebraic operations on matricies are defined by keeping in mind that T(x) = Ax.
- Equality
- For matricies A and B, say that A = B if aij == bij.
- Consequnce: A = B → A and B have the same size.
- Addition
- For mxn matricies A and B, the sum f A and B (A+B) is the mxn matrix whose (i,j)-entry is aij + bij.
- Matricies of inequal dimensions is not defined.
- Scaling
- For A an mxn matrix, the matrix rA (where r is in R), is the mxn whose (i,j)-entry is r * aij.
- Negative Unary
- Defined as -A = -1 * A
- Subtraction
- Defined as A-B = A + (-B)
- Hadamard Product
- Multiplying matrices A and by doing: aij * bij.
- Multiplication
- If A is an mxn matrix, B is an nxp matrix, then AB = [Ab1 ... Abp]
- Transpose
- For A, an mxn matrix, define the "Transpose of A", denoted by AT, is the nxm matrix whose (i, j) entry is aji.
- This just turns the rows in A into columns.
- (AT)T = A
- (A+B)T = AT + BT
- (rA)T = r(AT)
- (AB)T = BT AT
Theorem
If A, B, and C are matricies, and r, s are scalars, then...
- A+B = B+A (Commutative)
- (A+B)+C = A+(B+C) (Associative)
- A+0 = 0+A = A
- r(A+B) = rA + rB
- (r+s)A = rA + sA
- r(sA) = (rs)A
Why is matrix multiplication the way it is?
Based on the idea of function composition. For example, f(x) = y, and g(y) = z, thus g(f(X)) = z!
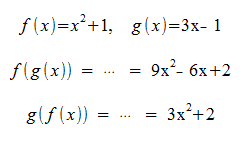
Now let's examine two Matrix transformations that map a vector x from Rn to Rm with some matrix A, and then that result can get mapped to Rp with some matrix B! This looks a lot like function composition.
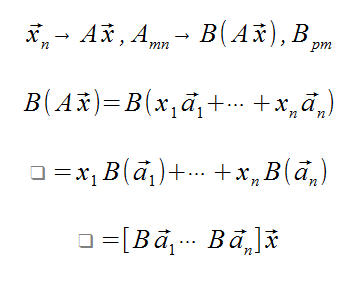
Notice the first transformation is the last matrix (B in this case), just like function composition!
Not only is BA ≠ AB, but in some cases, BA may be undefined!
Row-Column Rule
Define vector dot products as the sum of multiplying two vectors entry-wise. x dot y = sum (from 1 to n) of (xi * yi)
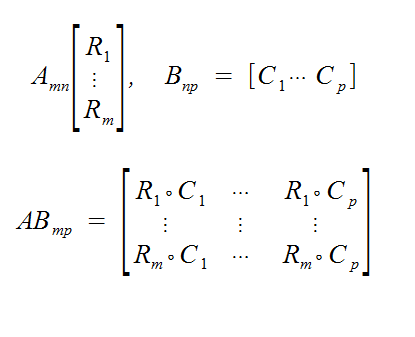
Theorem
- We can do associative things with matrix multiplication. A(BC) = (AB)C
- A(B+C) = AB + AC. (Left Distributive)
- (B+C)A = BA + CA. (Right Distrbutive)
- r(AB) = (rA)B = a(rB)
- Identitiy Matrix I, ImA = A = AIn
Notice that A(B+C) = AB + AC, and (B+C)A = BA + CA, but we cannot say that A(B+C) = BA + CA!
Powers of matricies
Suppose that A is a square matrix, then the following are defined: AA, A(AA), (AA)A. They are commutative too!
Therefore, we define A2 as AA, and a3 as A(AA), and so on.
Ak = A*A*A ...
And now then, Ak * Al = Ak + l if k and l are greater than 1.
For convienience, we define A1 as A. And A0 as the identity matrix.
Multiplying by diagonal matricies
If A is some matrix, and D is some disagonal matrix, then:
- AD results in A's columns getting scaled by the appropriate entry in D.
- DA results in A's rows getting scaled by the appropriate entry in D.
Matrix Inverse
Does there exist a matrix B such that B(Ax) = x for any x?
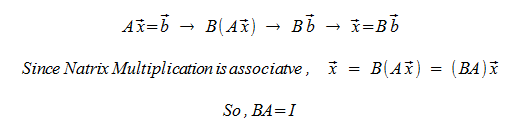
The Matrix B is unique.
Assume there's a matrix C, not equal to B, such that AC = CA = I.
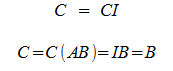
Why must it be square?
One could say that an mxn matrix A is invertible if there exists nxm matricies C and D such that CA = In and AD = Im. However, these equations imply that A is square and C = D.
Find a 2x2 Inverse Matrix
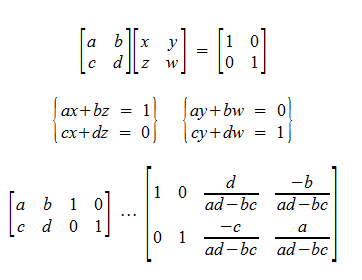
Theorem
If A is a 2x2 matrix, then ad-bc (product of diagonal entries minus product of non-diagonal entries) ≠ 0, then A is invertible and:
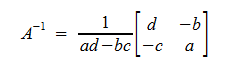
Conversely, if the scenario above is equal to 0, then A is not invertable.
A matrix A is invertible if, and only if, the vectors making up the matrix form a linearly independent set!
Example
Determine if A is invertible, and if it is, find the inverse.
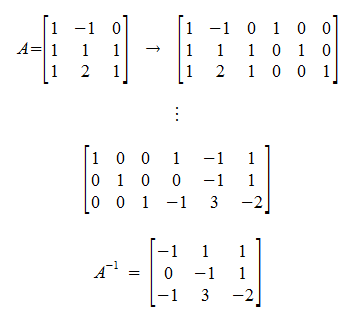
Theorem
If A is an nxn matrix, then A is invertible if, and only if, [A|I] ~ [I|B], therefore A is invertible iff A ~ I, and its inverse is B.
Setup
If A is an nxn matrix, then A is invertible iff there exists an nxn matrix X = [x1, ..., xn] such that AX = I.
- ↔ A[x1, ..., xn] = [e1, ..., en]
- ↔ [Ax1, ..., Axn] = [e1, ..., en]
- ↔ Ax1 = e1, ..., Axn = en are feasible
Lemma
(a "Lemma" doesn't look like much, but still acts like a theorem and can have big implications.)
If Axi = ei is consistent for every i from 1 to n, then the linear system Ax = b is feasible for every vector b in Rn.
Proof

Following the set-up and the Lemma, A is invertible iff Ax = b is feasible for every b in Rn, which is to say, A is invertible iff A has a pivot in every row.
Theorem
- If A is invertible, then (A-1)-1 = A
- Because -1 * -1 = 1, and A1 = A
- If A and B are invertible, then AB is invertible and (AB)-1 = B-1A-1
- Because in matrix transformations, we do B and then A, so to undo this we have to undo B first, then undo A.
- If A is invertible, AT is invertible, and (AT)-1 = (A-1)T.
- If k is any natrual number, then A-k = (Ak)-1.
Invertible Matrix Theorem
Let A be an nxn matrix, Then the following are equivalent (all true or all false)
- A is invertible.
- A is row-equivalent to the Identitiy.
- Any ecehlon form of A has n pivot positions.
- Ax = 0 has only the trivial solution.
- The columns of A are linearly independent.
- Ax = b is consistent for every vector b in Rn
- The span of the columns of A cover all of Rn
- There exists a matrix C such that CA = I.
- There exists a matrix D such that AD = I.
- AT is invertible.
- The determinant of A is not 0.
- 0 is not an eiganvalue of A.
Theorem
If A and B are square matricies, such that AB = I, then BA = I.
Proof
(Claims)
- The columns of AB are Linearly Independent.
- The columns of B are Linearly Independent.
- The columns of A are L.I.
- BA - I = 0.
Claim 1: If not, there exists a non-zero vector x such that (AB)x = 0, but (AB)x = Ix = x, thus a contradiction.
Claim 2: If not, there exists a non-zero vector x such that (B)x = 0, but (AB)x = A(Bx) = A(0) = 0 = x (from previous claim).
Claim 3: If not, there exists a non-zero vector y such that Ay = 0. Since Bx is feasible for every vector b in Rn, then there is a non-zero vector x such that Bx = y. Now, 0 = Ay = A(Bx) = (AB)x = x, thus a contradiction.
Claim 4: AB = I, so ABA = A, so A(BA-I) = 0. If not, then BA-I has a nonzero entry and hence a non-zero column. This can't happen because A is L.I.
Elementary Matricies
Wouldn't it be nice to find a matrix to simplify our row-operations?
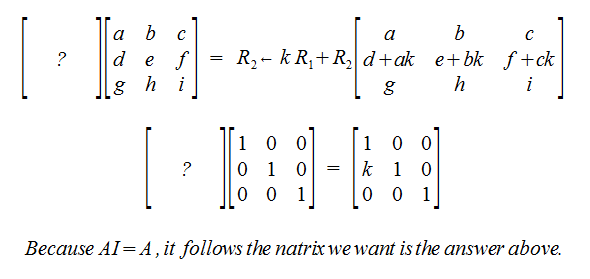
Adding rows by some scalar:
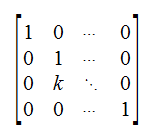
Row Interchange:
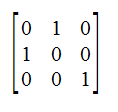
Row Scaling:
Matrix Factorizations
Theorem
If A is an nxn triangular matrix (upper, lower, or both), then A is invertible ↔ every diagonal entry is non-zero. (Obvious Proof)
Proposition
If A and B are square lower triangular matricies, then AB is lower triangular. Same for upper triangular.
Why Factor?
What's is the most efficient way to solve A x1 = b1, A x2 = b2, etc...
Direct correlation to processing verticies and graphics!
Fact
If Elementary matrix that corresponds to Row Replacement (Adding with a scalar multiple of another row), then E-1 exists with -k nistead of k.
LU-Factorization
Theorem
If A is an mxn matrix that can be row-reduced to echelon form without row interchanges, then there is an mxm unity lower triangular matrix L, and an echelon matrix U of A such that A = LU.
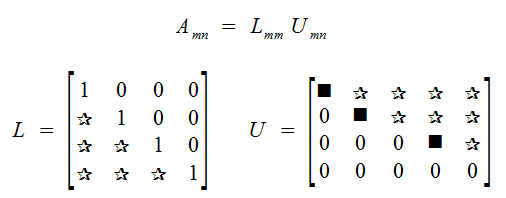
Proof
By Hypothesis, there exists lower-triangular matricies E1, ..., Ep (corresponding to Row Replacements) such that (Ep ... E1) A = U.
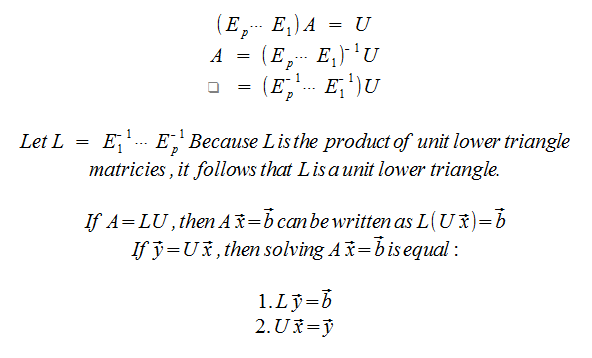
How do it?
Rules for reducing A- Only use Row Replacements (Row + c * otherRow)
- Only use Rows below the row you're replacing (creating upper triangle)
- Reduce A to an echelon form U using the rules above
- Place the entries in L such that the same sequence of row operations reduces L to I.
Subspaces of Rn
Any plane in R3 that contains the zero-vector, will look and act like R2.
Theorem
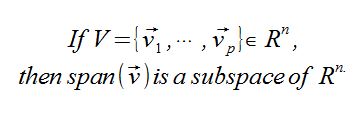
Proof
- Clearly the zero vector is in the span.
- Suppose that u and v are in the span of V, thus there is a Linear Combo of V to result in u and v.
- Clearly u+v are in the span as well.
- And again, we can scale the vector u and this is also in the span.
IS there a span in Rn that is not a subspace?
Fundamental Subspaces of a Matrix
If A is an mxn matrix, then Col(A) is a subspace of Rm (because, as we stated above in the theorem, a span of vectors is a subspace).
If A is an mxn matrix, then the Nulspace of A is a subspace of Rn (not m!).
Basis
A basis for a subspace H of Rn is a linearly independent set in H that spans H.
The columns of the nxn identity matrix form what's known as the standard basis for Rn.
To find a basis for the null space
- Row-Reduce the matrix A with the homogenous form (Ax = 0) to its Reduced Echelon Form
- Put the solution set in parametric vector equation form to get your Linearly Independent Spanning Set.
Example:
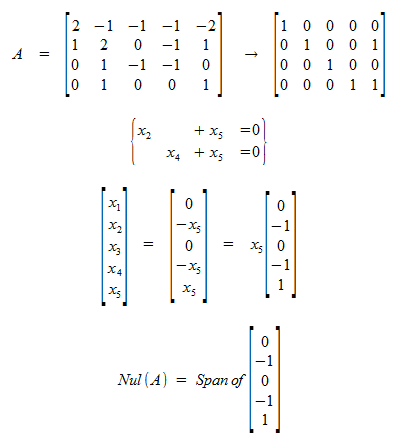
To find a column basis
- Bring a matrix to its Reduced Echelon Form.
- Each pivot column in the matrix means the corresponding column (vector) in the original matrix will form the basis for the Column Space.
Why is not the R.E.F. matrix's columns that are the basis, but the original matrix's?
Row operations change the column space, but the solutions (in terms of generic vectors of the Linear System) remain the same.
Dimension of a Matrix
First off, let's define the word "dimension&qout;.
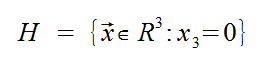
We'd like to say that the dimension of H is 2, even though it lives in R3.
Theorem
Let H be a subspace of Rn and let B (a set of vectors) be a basis for H.
If vector x is in H, then there are unique scalars such that the vector x can be written as a linear combination of the vectors of B.
Proof
Because B is a spanning-set, the existance of these scalars is guaranteed. Now, for uniqueness... Assume there are another set of scalars where at least one is not equal to the previously stated scalars, such that these scalars can be written as a linear combination of the vectors of B.
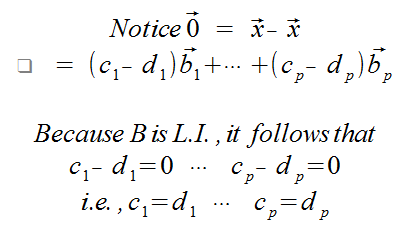
For every vector x in H, the coordinates of x relative to B are the unique scalars such that x = Bc.
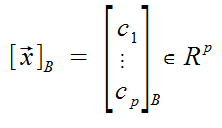
The vector x (as above) is called the B-coordinate vector of the original vector x.
So what is this mess?
Imagine H as the the image above in this section. A basis for H is the 3x3 Identitiy matrix with the 3rd column 0.
We can use the definition above to say:
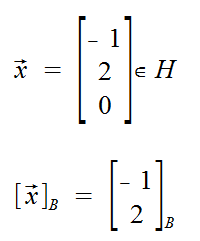
Consider the correspondence f: H → Rp where vector x → [x]B.
It can be shown that f is a bijective mapping that preserves linear combinations. This means the function is linear (so you can use algebra happily).
Such a mapping is called an isomorphism, and we say that H and Rp are isomorphic (Same Structure). This is the mathematical precision of saying "H looks and acts like R2, so we can just go play in R2 and be happy.
Remark
Because there infinitely many bases for H, and the dimension we isomorph H into depends on the number of vectors in the base, how can we truly say H is an isomorph of Rp. Well, a basis has to be a Linearly Independent set, so therefore it will always have the same number of vectors.
Convention
The dimension of the zero-vector is equal to 0.
Rank of a Matrix
Consider a 3x5 matrix with pivot columns in 1 and 3. The Rank(A) = 2. Nullity(A) = 3.
Theorem
If A is an mxn matrix, then the rank(A) + nullity(A) = m
Determinants
Recall the solution for determining if a 2x2 matrix is invertible.

- Invertible can be called non-singular
- Non-Invertible can be called singular
Now, wouldn't it be nice if there is a determinant for matrices that are not 2x2? Calculating them is way too complex though. Forexample, the determinant for a 3x3 is:
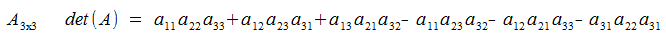
2x2 had 2 terms, 3x3 has 6 terms... Calculating the determinant requires n-factorial terms, which is the worst big-O ever!
Anyway, notice that A is invertible iff det(A) ≠ 0.
The ugly terms above can be rewritten like so:
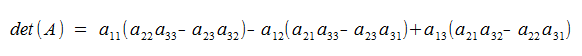
Notice that within each parenthesis, the determinant depends on the determinants of the 3 unique 2x2 sub-matrices!!
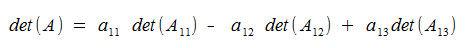
Where Aij is the matrix obtaind from A by deleting the ith row and the jth column of A.
size(Aij) is (n-1) x (n-1)
For n >= 2, the determinant of the nxn matrix of A [aij], denoted by det(A), or deltaA, or |A|, is given by:
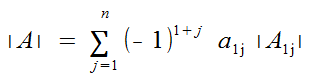
Using Cofactors, we can rewrite this more simply.
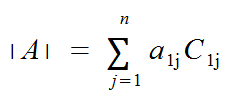
Example
Find det(A).
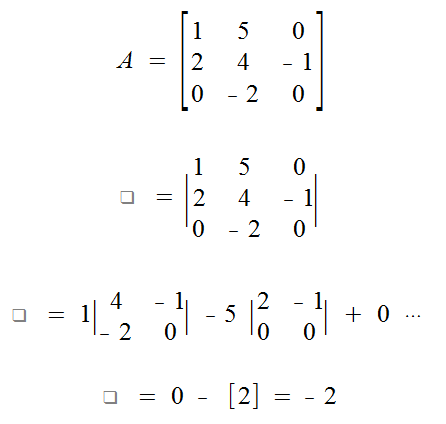
Theorem
If A = [aij] is an nxn matrix, then we can take a determinant with either the rows or the columns.
- A determinant by going across a row is called: a cofactor expansion across row i.
- A determinant by going down a column is called: a cofactor expansion down column j.
You can actually use any row and column to "go along"!
The 1's listed above in the equation for a determanent can be repalced with i to indicate a row. The i-variable never changes through the summation though, so it's fixed.
Notice that Triangular Matricies make this easier
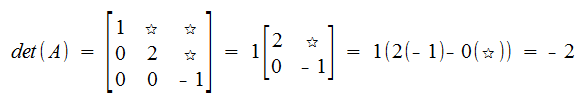
Theorem
If A is triangular (upper or lower) then:
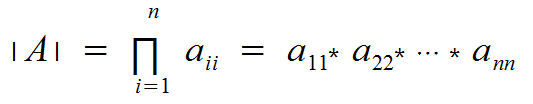
The problem is that row operations change the column space of the matrix, so even though we can make a triangular matrix, we can't use that to calculate the determinant.
Properties of Determinants
How do Row-Ops Affect Determinant?
2x2 Matricies
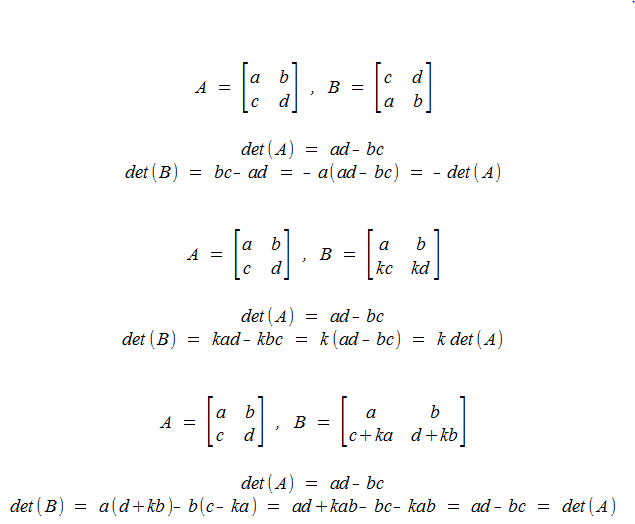
- If A~B via Ri ↔ Rj, then - det(A) = det(B)
- If A~B via Ri ← kRi, then k det(A) = det(B)
- If A~B via Ri ↔ Ri + k Rj, then det(A) = det(B)
Example

A faster way to calculate the determinant
Suppose that a square matrix A has been row-reduced to an echelon form U via row-replacements (R becomes R + k someOtherRow) and row-interchanges (which is always possible). If there are r row-interchanges performed, then det(A) = (-1)
Because U is upper-triangluar, if follows that the determinant of U is the product of its diagonal entries.
If U is invertile, then its diagonal entries are all non-zero, and if U is non-invertible, then there must be at least one zero value in the diagonal entries.
Theorem
The square matrix A is inverible iff det(A) ≠ 0
Theorem
If A is an nxn matrix, then det(A) = det(AT). Intuitively, this is because if you calculate the determinant by going down A's jth column, this is equal to calculating the determinant by going down AT's jth row.
Theorem
If A and B are square matricies of the same size, then det(AB) = det(A) det(B).
Maths
- det(AB) = det(A) * det(B)
- det(A+B) ≠ det(A) + det(B)
Eigenvectors & Eigenvalues
Why are these important?
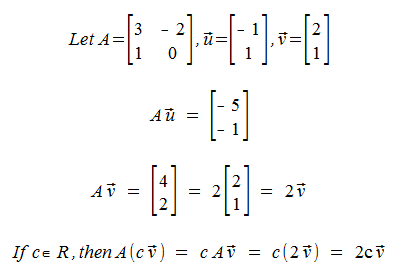
Notice that the mapping Av is just scalaing the vector v by 2! This is just weird, given this doesn't happen for other vectors (like u).
This also means any scalar of v will get scaled by 2 when mapped by A, so the Eigenspace is the vector v.
The definition of Eigenvector and Eigenvalue means that for one eigenvalue, there may be multiple eigenvectors. As in the example above, any scalar of v is an acceptable eigenvector for the eigenvalue 2.
Now, are there multiple eigenvalues for a single eigenvector? No, because by the definition, Ax = lx, so having Ax also = ux, is impossible.
Example
Verify that 7 is an eigenvalue for:
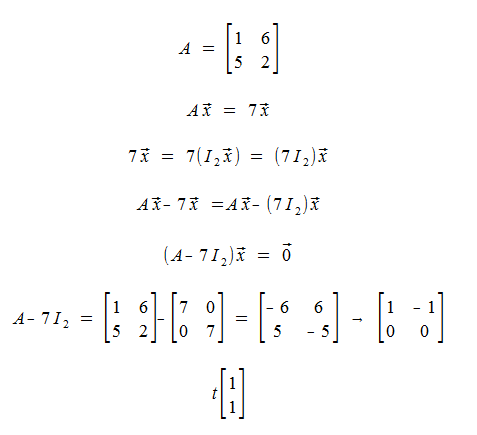
Any vector of the form t, is an eigenvector corresponding to 7.
Theorem
From the previous example, notice that lambda is an eigenvalue for A iff the Homogeneous Linear System (A - lambda In)x = 0 has a nontrivial solution.
The set of all solutions to this H.L.S., is the Nullspace of that equation: Nul(A - lambda In) and this is called the eigenspace of A corresponding to lambda.
Example
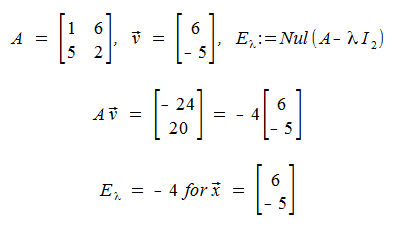
Example

Theorem
The eiganvalues of a triangular matrix are its diagonal entries.
Proof
Consider the upper-triangular case. If A is an upper triangluar matrix, then A - lambda I, results in ann - lambda for all diagonal entries. The upper entries in A don't change, and the 0s below remain 0.
Thus, (A - lambda I) has a nontrivial solution iff aii - lambda ≠ 0. And further, aii is an eiganvalue for A. This also works for lower triangular matricies.
We cannot use row operations to make a matrix into a triangle form to get its eiganvalues, because row operations ruin the original matrix's eiganvalues.
Theorem
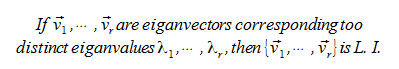
Proof
Assume that there exists scalars, such that a linear combination of some of the vectors of v with respect to the scalars, results in a vector already in the set. This means one of the vectors in v is a linear combination of the others, so it's extra, so v would be L. D.
From here, basically we play with it by multiplying it by the matrix A and substituing lambda, and it results in a contradiction where it states that one of the vectors in v must be 0, which we already said wasn't true.
The Characteristic Equation
Given an nxn matrix A, how do we compute its eiganvalues? Use the determinant of A to test for invertiblity, and thus for non-trivial solutions of Nul(A - lambda I)!
It is sometimes better to express it as: Nul(lambda I - A).
Example
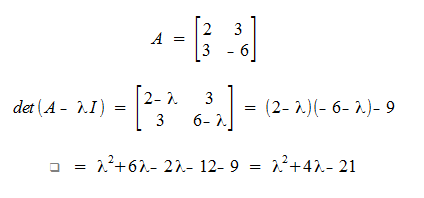
Thus Lambda is an eiganvalue of A iff:
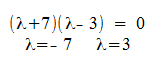
- Finding the eiganvalues of a 2x2 matrix is equivalent to solving a quadratic equation.
- The soltions of ax2+bx+c = 0 (where A > 0 (actually a is always 1 for us!)) are given explicitly by the quadratic formula
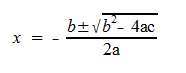
Example
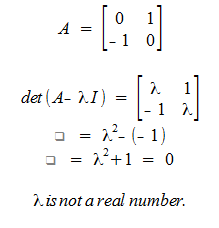
nxn matricies have exactly n eigan values. This is proved by showing that the characteristic equation boils down to a polynomial of the nth degree, and there is a proof that a polynomial of n-degrees has exactly n roots. This means the characteristic equation has n roots.
However, Galois Theory states that degrees of 5 or higher cannot be expressed like a quadratic equation, so actually the eiganvalues of an nxn matrix cannot be computed explicitly.
Characteristic Polynomial
Rather than state the determinant of lambda I - A to 0 to solve for a particular eiganvalue, we call lambda 't', and don't set it to 0 explcitly. This results in a polynomial with varius t variables and makes it really easy to see which values will result in the equation being 0.
Matrix Similarity
A special group of matricies:
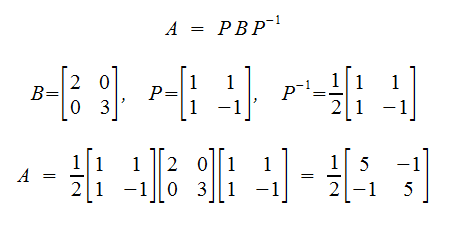
further, if A and B are similar, then A and B have the same eigenvalues!
This is the technique used to find eigenvalues of large matricies because we can't express large matricies as a polynomial (easily).
Diagonalization
A fundamental goal in matrix theory is to write most matricies in the form P D P-1, where D is a diagonal matrix. Most matricies are similar to a diagonal matrix.
This is super cool, because if we're doing a mapping with a vector x, then we're mapping x to a different basis (P-1), then hit it with a diagonal matrix (super easy to calculate and see what it does), then map it back to its original space wth P!
Theorem
A is diagonalizable iff A has n linearly independent eiganvectors. Morever, A = PDP-1, iff the columns of P are n linearly independent eigenvecotrs of A. The diagonal entries of D are the eiganvalues of A.
Proof

This argument can be proven by reversing the argument above, so it's an iff.
Example
Diagonalize (if possible) the matrix:

Note that we can create P by setting the eiganvectors in any order. Just as long as the order of the eiganvectors match the order of the eiganvalues.
Example
Non-diagonalizable matrix (Jordon Block).

Theorem
An nxn matrix with n distinct eiganvalues is diagonalizable. HOWEVER, if an nxn matrix is diagonalizable, it does not contain distinct eiganvalues.
Proof
Follows the prooof way above that states if there is a lineraly indepent set of eigan vectors, then there is a L.I. set of eiganvalues, thus can be diagonalized.
Length
Length in R2 is easy, d2 = sqrt(a2 + b2), but for any dimensional space, how do we get the length of a vector?
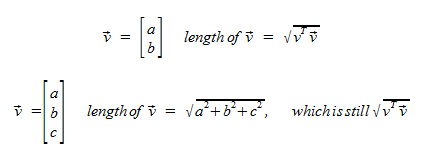
Distance in Rn
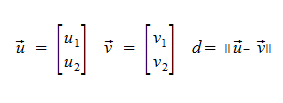
Inner Product
Also called the dot product, is the product of a vector u and v, calcuated by uTv. The result is a scalar (R1).
For the purposes of this kind of multiplcation, we call vectors an nx1 matrix, so that uTv is a matrix multiplcation, which results in a 1x1 matrix, or a scalar.
Theorem
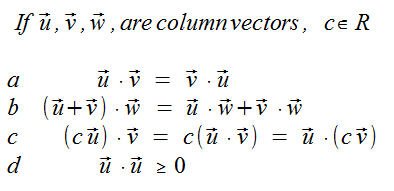
For a vector v, a column vector, we define the length (norm) of v as the nonnegative quantity ||V|| = sqrt(vT v)
Proposition
If vec v is a column vector, and c is any real number, then
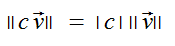
If vec v is any nonzero vector, thenthe length of a vector u is one by this:
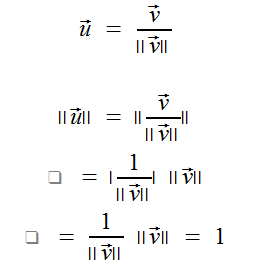
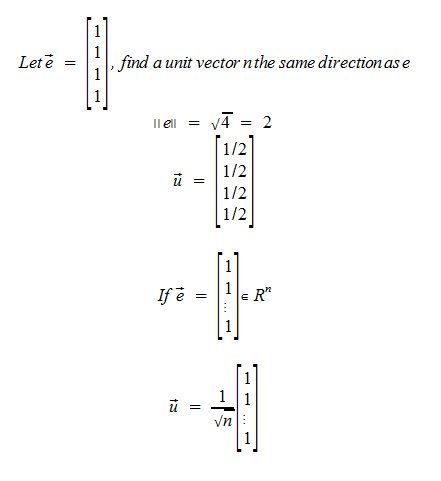
Matricies and Vectors
Matrices behave like vectors. You can scale them, there's a 0-matrix like the 0-vector, and you can actually define the distace of a matrix...
Orthogonality
We want to generalize the notion of perpendicularity to Rn.
We define two vectors to be othrogonal (based on geometry), as the distance from v to -u must be eqal to the distance from v to u. This is only true if u dot v is 0.
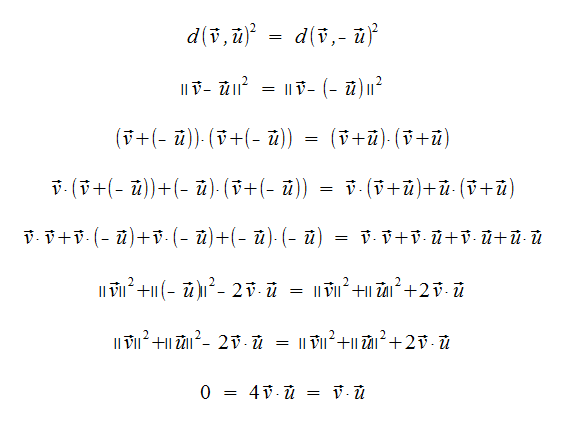
Definition
We say that the vectors u and v of Rn are orthogonal (to each other) if u dot v = v dot u = 0
As a consequence, every vector is orthogonal to the zero-vector.
Now, if u dot v is 0, then any scalar multiple of either u or v must be orthogonal.
Orthogonal Complement
(Reminder) A subspace is a subset within a space that looks and acts like a lower dimension. Note that a subspace of R3 is a set of vectors in R3, but it looks and acts like some unspecified lower dimension. It is still a subspace of R3.
If W i a subspace of Rn, then the orthogonal complement of W, denoted W⊥, = {vec z in Rn : z dot w = 0, for every w in W}.
- If W is a subspace of Rn
- vec x is in W⊥ iff x is orthogonal to every vector in a spanning set of W
- W⊥ is a subspace of Rn
- (W⊥)⊥ = W
- In R3, the Perp of a plane is a line, and the perp of a line is a plane.
Orthogonal Sets
A set of vectors {u1, ..., un} in Rn is called orthogonal or an orthogonal set if ui dot uj = 0 whenever i ≠ j.
The columns of the identity matrix form an orthogonal set.
Example
Show that the columns of the Hadamard matrix are orthogonal.
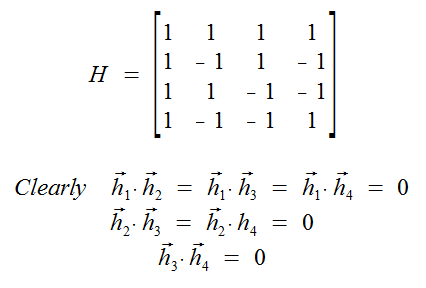
Aside
Hadamard matricies are formed by placing a 1 in a 2x2 matrix, then a -1 in the bottom-right position. To make a bigger matrix, repeat this pattern with this 2x2 matrix to make a 4x4 matrix. Now you could make a 8x8, 16x16...
- HT H = nI
Orthogonal Sets
A set of vectors U is an orthogonal set if ui dot uj = 0, whenever i ≠ j.
For example, the columns of the Identity matrix, or the columns of the Hadamard Matrix.
Why does this matter?
If U is orthogonal, then U is Lineraly Independent, and hence a basis for span(U).
Proof
The coverse is clearly not true. Suppose that there are scalars C (not all zero) such that U dot C = 0. (In a L.I. system, only when all scalars are 0 is the solution).
Assume that ci ≠ 0
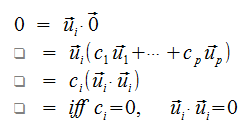
Orthogonal Basis
An orthogonal basis is an orothogonal Linearlly Independent Spanning Set.
Theorem
If U is a set of vectors in Rn and is an orthogonal basis, and W is the span(U), then for any vector w in W...
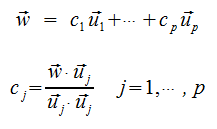
This means we don't have to solve a linear system to find out the scalars for each x.
Proof
Because U is a basis, there are unique scalars C such that vector w = C dot u.
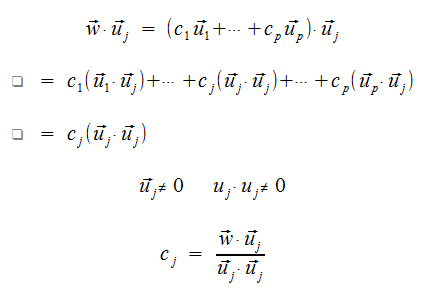
Complexity
This algorithm is linear, wheras solving for non orthogonal matricies, it's exponential! (n3)
Orthonormal Set
An orthogonal set, but the vectors are also all unit vectors. Given an orthogonal set, it's very easy to turn it into an orthonormal set.
Theorem
If U is an mxn matrix, then U has orthonormal columns iff UTU = In
Proof
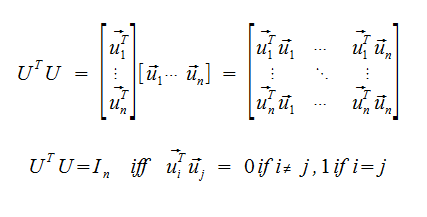
Glossary
- Basis
- A spanning set of vectors that's linearly independent and only contain 1s and 0s, they also span all of their dimension.
- Characteristic Equation
- The scalar equation det(A - lambda I) = 0, is called the characteristic equation.
- Consistent
- System has a solution.
- Coefficient Matrix
- Just write down the coefficients for the variables.
- Since all we do is mess with the coefficients anyway, this is so much cleaner.
- Coefficient Matrix, Augmented
- Includes a bar after the last column that includes the solution.
- Does not affect the size convention of the matrix.
- Cofactor
- Given A = [aij], the (i, j)-cofactor of A, denoted by Cij, is given by Cij = (-1)i+j det (Aij).
- The cofactor is just a number.
- Column Vector
- A matrix with only one column.
- For example, when n = 2, u (with arrow) = [3 1] (in 2 rows).
- Columnspace
- The columnspace of a mxn matrix, denoted by Col(A), is the span of the columns of A
- This is just the span of the columns of A, and thus the range or image of the TF matrix of A.
- If T maps Rn to Rm, defined by T(x) = Ax, then R(T) = Col(A)
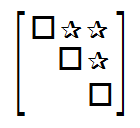
- Diagonal Matrix
- A square matrix whose off-diagonal entries are 0.
- A special type of Reduced Ecehlon Form matrix (the 1s are stars, not just 1s)
- Diagonalizable
- A square matrix A that can be written in the form: A = P D P-1
- Echelon Form
- A matrix that satisfies these conditions:
- All non-zero rows are above any zero rows LinearInDependence
- Each leading entry of a row is in a column to the right of the leading entry of the row above it.
- All entries in a column below a leading entry are zeros.
- Denoted by U
- Eigenvalue
- The scalar lambda in an Eigenvector is called an eigenvalue of A.
- Eigenvector
- Eigen means 'same' in German.
- An Eigen vector of a square matrix A is a nonzero vector x such that Ax = lambda x for some lambda in R (or lambda could even be complex!).
- The vector x is called an eigenvector corresponding to lambda.
- (lambda, x) is called an eigenpair for A.
- We exclude the zero vector for x because it's trivial. It will always be present, we're looking for other eigenvectors.
- Elementary Matricies
- Row operations can be performed on a matrix via left-multiplication by elementary matricies.
- Factor
- Let A be an mxn matrix, If there is an mxp matrix B and a pxn matrix C such that A = BC, then B and C are factors of A and the product of BC is calle da factorization of A.
- Free Variable
- One of the columns of a coefficient matrix is not a pivot column.
- Function
- A function is a relation in which for ever d in some set D, there is exactly one r associated to it.
- In other words, one unique input results in the same output every time, not different output.
- f:D→R
- Homogeneous L.S.
- A Linear System of the form Ax = 0.
- This is just the Matrix Function where b == 0.
- There is always a solution because the vector x can be all 0s.
- There are inifinite solutions if the matrix A has a free variable.
- Inconsistent
- System does not have a solution.
- Inverse Matrix
- An nxn matrix A is said to be invertible if there exists an nxn matrix B such that AB = BA = I
- Denoted by A-1.
- This is because we're essentially saying: A A-1 = A1 A-1 = A0 = I
- Image of x
- See Transformations
- T(x) is called the image of x, and the set of all images is called the range, or image, of T.
- R(T) is called the range (or image) of T.
- R(t) = span ({a1 ... an}).
- It's called an image because the vector is being projected! It's "casting a shadow".
- Linearly Dependent
- A set of vectors where the Matrix Equation results in 0 for an x-vector that is not all zeros.
- Linearly Independent
- The set {a1, ..., an} is said to be Linearly Independent if the vector equation (x
1 a1 + ... = 0) has only the trivial solution (x-vector is all 0s). - A set of vectors that only has a Matrix Equation of 0 if the x-vector is 0.
- Linear System
- A finate collection of lienar equations in the same variables.
- Main Diagonal
- Regardless of size, it's the entries aii of any matrix A.
- Matrix
- A rectangluar array of numbers.
- The numbers in the array are called its entries.
- Leading Entry
- A row (or column) that refers to the leftmost (topmost) non-zero entry.
- In a non-zero row
- N-Tuple
- English ways of saying 'n' versions of double, triple, quads, etc.
- Non-Zero Row/Column
- A row (or column) with at least one entry thats not a 0.
- Norm
- The length of a vector.
- Nullspace
- The nullspace of an mxn matrix A, denoted by Nul(A), is defiend by all vecotrs in Rn such that Ax = 0.
- The nullspace of A is the solution set of the homogeneous matrix of A.
- Nullity
- Very similar to Rank, but it's the dimension of the null-space of A.
- Off Diagonal Entries
- Entries in a matrix that are not in the main diagonal.
- Overdetermined
- More equations than variables.
- m > n
- Parallelogram Law
- The fact that you can add two vectors together to result in a third vector.
- In 3D, this law manafests as a plane's normal being added together to result in a new normal for a new plane.
- Patametric Vector Equation
- An equation of the form (vectors x, u, and v; scalars s and t): x = su + tv.
- Pivot
- A nonzero number in a pivot position.
- Pivot Columns and Rows
- A column or row that contains a pivot position.
- Pivot Position
- in a matrix A, is a location that corresponds to a leading entry in the R.E.F. of A.
- Rank
- The rank of the mxn matrix A, denoted by rank(A), is defined by rank(A) = dimension(Col(A))
- This is just another name for the dimension of the column space of a matrix.
- Reduced Echelon Form
- If a matrix in echelon form satisfies the following additional condiations:
- All leading entries are 1s
- Each leading entry is the only nonzero entry in its column.
- Row Equivalent
- Two matrices (A and B) are row-equivalent if there is a finite sequence of row operations that transforms one matrix into the other.
- Denoted by ~
- Size Convention
- Rows by Columns.
- Solution
- Any ordered n-tuple that satisfies the linear system. Plug in numbers, every equation is true!
- Solution-Set
- Collection of all possible solutions to a linear system. May be empty.
- Two linear systems are equal if they have the same solution set.
- Span
- Given a list of vectors in a set dimensional space. The span of these vectors is the set of all possible linear combinations of the vectors where each vector has a scalar (possibly different for each vector). For example, this forms a plane with 2 vectors in either 2D or 3D space.
- Given vectors v1, ..., vp in Rm, the span of v1, ..., vp is denoted by the span({v1, ..., vp}), is the set of all possible linear combinations of v1, ..., vp.
- span({v1, ..., vp}) = {y in Rm where y = the sum of civi where c is in R1
- A mathematical way of saying we're running functions on an array.
- For a 2D vector, this results in a plane because we can scale and then add any two vectors to result in a new vector anywhere on the plane.
- Subspace
- A subspace of Rn is any subset H of Rn such that:
- The zero-vector is in H
- u + v is in H, whenever u and v are (separately) in H
- cu is in H, whenever u is in H and c is a scalar.
- It's a subset of space in Rn that looks and acts like some lower dimension or itself.
- Transformation
- A transformation (or function or mapping) from Rn to Rm is a rule that assigns to each vector x in Rn to a vector T(x) in Rm.
- A transformation is linear if...
- T(u + v) = T(u) + T(v) for every vector u and v in Rn.
- T(cu) = cT(u).
- The matrix transformations are linear transformations.
- And all linear transformations are matrix transformations!
- Triangular Matrix
- A matrix with all 0s in either all above the main diagonal, or below the main diagonal.
- Upper Triangular if aij = 0 whenever i > j
- Lower Triangular if aij = 0 whenever i < j
- Underdetermined
- Fewer equations than variables.
- m < n
- Unique
- A linear system has one, and only one, solution.
- Unit Vector
- A vector with a length/norm of 1.
- Vector Space
- A collection of all column vectors with n entries, and is denoted by Rn.
- Zero Matrix
- A matrix of all 0s. 0mxn
- Zero Row/Column
- A row (or column) with all 0s
- Zero Vector
- A vector of all zeros.
- Denoted by O2 for a 2D vector.
Syllabus
- Generally just chapters 1-6 from text book. Not so much application from the book.
- Canvas will only be used for grading.
- Assignments will be emailed out via pdf. Print them out, write on them, and hand-em-in.
- Homework is not graded.
- Use LaTeX "word processor" for practice! Industry standards and such.